Introduction:
Welcome back to the second part of our series on bit manipulation. In the first part, we explored the basics of bit manipulation, including binary operators and determining odd or even numbers using the "&" operator. If you haven't read it yet, you can check it out here. In this continuation, we will delve deeper into the world of bit manipulation and uncover more advanced techniques. Get ready to expand your knowledge and unlock new possibilities with JavaScript!
In this blog, we will cover additional topics that build upon the foundation established in the first part. We will explore techniques such as calculating the negative of a number using bitwise operators, finding the element that appears only once in an array, manipulating specific bits, and more. By the end, you will have a solid understanding of advanced bit manipulation techniques and how to apply them effectively in your JavaScript code.
Let's dive in and continue our journey of mastering bit manipulation!
Calculating the Negative of a Number using Bitwise Operators:
To calculate the negative of a number using bitwise operators, we can utilize the 2's complement method. It involves two steps:
Complement the bits: In this step, we flip all the bits (0s become 1s and 1s become 0s) of the given binary number.
Add 1: After complementing the bits, we add 1 to the resulting binary number.
The result obtained is the negative of the number.
But how?
To provide further explanation of the 2's complement method, let's consider the example of the decimal number 10 and its binary representation in an 8-bit system.
In an 8-bit system, a single byte can store up to 8 bits. To represent the decimal value 10 in binary using 8 bits, we would write it as 00001010.
Now, let's calculate the negative representation of 10 using the 2's complement method.
First, we know that in a 2's complement system, the negative representation of a number can be obtained by taking the complement of the number and then adding 1 to it.
Starting with the binary representation of 10: 00001010, we will complement each bit, flipping 0s to 1s and 1s to 0s.
Complement of 10: 11110101
Now, we need to add 1 to the complemented value. To do this, we write 1 in binary: 00000001.
Adding 1 to the complemented value: 11110101 + 00000001 = 11110110
The result, 11110110, is the negative representation of the decimal number 10 in a 2's complement system.
To understand why this method works, let's consider the significance of the leading bit in an 8-bit system. In a signed number representation, the leading bit (leftmost bit) is used to indicate the sign of the number.
If the leading bit is 0, the number is positive, and if it is 1, the number is negative.
Normally, to make a number negative, one would simply subtract it from 0. That is what the indirect 2's complement approach accomplishes.
In our example, when we add the extra leading bit before 10000000, it does not change the value since it exceeds the capacity of the 8-bit system. Thus, we can rewrite 100000000 as 1 + 11111111 to make it fit within the 8 bits.
Now 11111111 + 1 - 00001010 (decimal number 10), Now rearranging this
11111111 - 00001010 + 1, solving 11111111 - 00001010 gives 11110101 which is equal to the complement of the number. As a result, subtracting any integer from a binary representation of 1's gives us the number's complement.Now add the balance of 1 to it. 11110101 + 1 gives 11110110, which is -10 in decimal.
By following these steps, we obtain the negative value of the original number. Let's demonstrate this with an example using the number 7:
function calculateNegative(num) {
const complement = ~num + 1;
return complement;
}
const number = 7;
const negativeNumber = calculateNegative(number);
console.log(`The negative of ${number} is: ${negativeNumber}`);
Output: The negative of 7 is: -7
In this example, we use the bitwise NOT (~) operator to complement the number and then add 1 to obtain the negative representation.
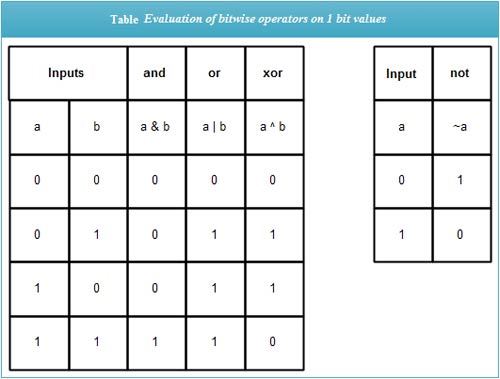
- Finding the Element that Appears Only Once:
To find the element that appears only once in an array where all other elements appear twice, we can utilize the XOR (^) operator. XORing an element with itself results in zero, effectively canceling out the pairs, and leaving us with the element that appears only once. Here's an example code in JavaScript:
function findSingleElement(arr) {
let result = 0;
for (let num of arr) {
result ^= num; // XOR operation
}
return result;
}
const array = [2, 4, 6, 4, 2, 8, 6];
// XOR of the same number cancels out to give 0.
const singleElement = findSingleElement(array);
console.log(`The element that appears only once is: ${singleElement}`);
Output: The element that appears only once is: 8
How: Because XOR the same number gives 0. Refer to the image for understanding.
In this example, we XOR all the elements in the array, effectively canceling out the pairs and leaving us with the element that appears only once.
- Finding the ith Bit of a Number:
To find the value of the ith bit of a number, we can create a mask with a 1 at the desired position and use the bitwise AND (&) operator. Here's an example code:
function getIthBit(num, i) {
const mask = 1 << i-1; // Create a mask with 1 at the ith position
// Because a&b will return true if both are true. 0&1 => 0, 1&1 => 1, 0&0=>0.
return (num & mask) ? 1 : 0;
}
const number = 10;
const i = 2;
const bitValue = getIthBit(number, i); //mask will be 10
// 1010 (decimal)
// & 0010 (mask)
// 0010
console.log(`The ${i}th bit of ${number} is: ${bitValue}`);
Output: The 2nd bit of 10 is: 0
In this example, we create a mask with a 1 at the desired position (2nd bit) and use the bitwise AND (&) operator to extract the bit value.
Setting the ith Bit to 1:
To set the ith bit of a number to 1, we can create a mask with a 1 at the desired position and use the bitwise OR (|) operator (This will return true if any one value is true else false i.e., if the binary at ith position is 0, then 0|1 gives 1). Here's an example code:
function setIthBit(num, i) {
const mask = 1 << i-1; // Create a mask with 1 at the ith position
return num | mask; // Perform bitwise OR to set the ith bit to 1
}
const number = 5;
const i = 4;
const newNumber = setIthBit(number, i);
// 0101 (5 in decimal)
//| 1000 (mask)
// 1101
console.log(`Setting the ${i}th bit of ${number} to 1 gives: ${newNumber}`);
Output: Setting the 4th bit of 5 to 1 gives: 13
In this example, we create a mask with a 1 at the desired position (4th bit) and use the bitwise OR (|) operator to set the bit to 1.
Resetting the ith Bit of a Number:
To reset the ith bit of a number, we can create a mask with a 0 at the desired position and use the bitwise AND (&) operator. Here's an example code:
function resetIthBit(num, i) {
const mask = ~(1 << i-1); // Create a mask with 0.
return num & mask; // Perform bitwise AND to reset the ith bit
}
const number = 7;
const i = 2;
const newNumber = resetIthBit(number, i);
// & any binary with 0 gives 0. 1&0 => 0.
console.log(`Resetting the ${i}th bit of ${number} gives: ${newNumber}`);
Output: Resetting the 2nd bit of 7 gives: 3
In this example, we create a mask with a 0 at the desired position (2nd bit) by using the bitwise NOT (~) operator on a mask with 1 at that position. Then, we use the bitwise AND (&) operator to reset the bit to 0.
Explanation: When we perform a bitwise AND operation between a number and a mask where the bit we want to reset is 0, all the other bits of the number remain unchanged, while the bit we want to reset becomes 0 regardless of its initial value.
Conclusion:
Bit manipulation using bitwise operators offers powerful tools for performing operations at the binary level. In this blog, we explored common bit manipulation questions and their solutions using JavaScript. We covered topics such as calculating the negative of a number using the 2's complement method, finding the element that appears only once using the XOR operator, and manipulating specific bits using masks. By mastering these techniques, you can optimize your code and efficiently solve problems that involve bit manipulation in JavaScript.
