Understanding Bit Manipulation

Introduction:

1. Binary Representation: Before diving into bitwise operations, it's essential to understand how numbers are stored in binary form. Numbers in programming languages are represented in binary using a fixed number of bits, typically 32 bits (4 bytes) for integers. We'll explore the binary representation of numbers and how bits are used to represent values.

   

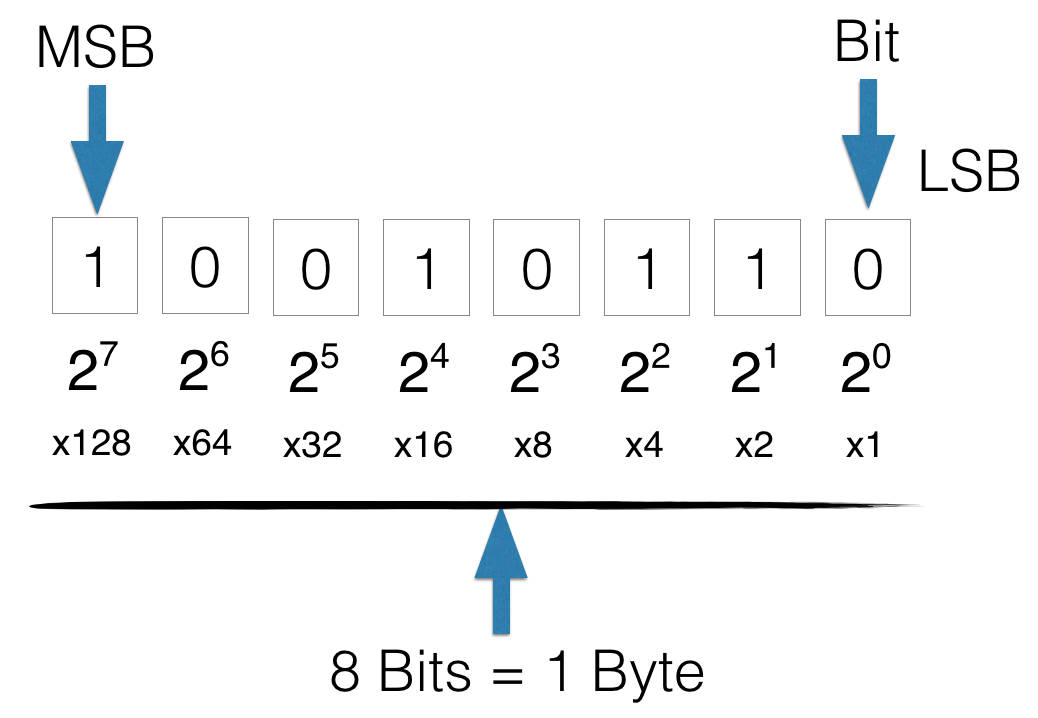
   Each bit in a binary representation can have either a value of 0 or 1, giving us a total of 2 possibilities per bit. In an 8-bit binary representation, we have 8 bits, so the total number of unique combinations is 2^8, which equals 256. This means we can represent 256 different numbers using 8 bits.

   • In an 8-bit signed integer representation, the range of values that can be stored is from -128 to 127. The 8 bits can represent a total of 256 different combinations, but one bit is reserved for the sign of the number, leaving 7 bits for the magnitude.

   • The leftmost bit, also known as the most significant bit (MSB), is the sign bit. If it is 0, the number is positive, and if it is 1, the number is negative. The remaining 7 bits represent the magnitude of the number.

   • With 7 bits available for the magnitude, the range of positive numbers that can be represented is from 0 to 127. The binary pattern 00000000 represents 0, and the binary pattern 01111111 represents 127.

   • For negative numbers, the sign bit is set to 1, and the remaining 7 bits are interpreted in two's complement form. The two's complement representation allows negative numbers to be expressed using the same bit patterns as positive numbers by flipping the bits and adding 1. The binary pattern 10000000 represents -128, and the binary pattern 10000001 represents -127.

   • Additionally, the least significant bit (LSB) is the rightmost bit, representing 2^0. It is the only bit that is not a power of 2. By checking the LSB, we can determine whether a number is odd or even. If the LSB is 0, the number is even, and if the LSB is 1, the number is odd.

2. Bitwise Operators: Bitwise operators work on individual bits of numbers. We'll discuss three fundamental bitwise operators: AND (&), OR (|), and XOR (^).

• The AND operator (&) compares the binary representation of two numbers bit by bit. If both corresponding bits are 1, it returns 1. Otherwise, it returns 0. Example: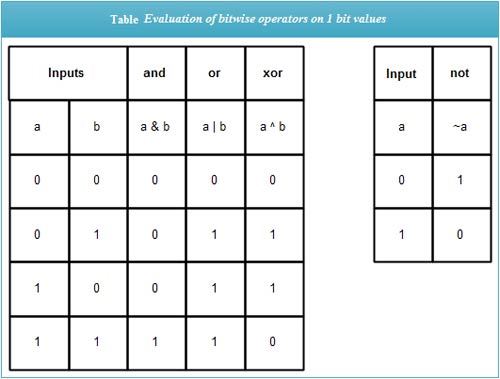

  

const a = 5;    // 0101 in binary
const b = 3;    // 0011 in binary
const result = a & b;   // 0001 in binary, which is 1 in decimal

• The OR operator (|) compares the binary representation of two numbers bit by bit. If at least one of the corresponding bits is 1, it returns 1. Otherwise, it returns 0. Example:

const a = 5;    // 0101 in binary
const b = 3;    // 0011 in binary
const result = a | b;   // 0111 in binary, which is 7 in decimal

• The XOR operator (^) compares the binary representation of two numbers bit by bit. If the corresponding bits are different (one bit is 0 and the other is 1), it returns 1. Otherwise, it returns 0. Example:

const a = 5;    // 0101 in binary
const b = 3;    // 0011 in binary
const result = a ^ b;   // 0110 in binary, which is 6 in decimal

1. Left Shift Operator: The left shift operator (<<) shifts the bits of a number to the left by a specified number of positions. It effectively multiplies the number by 2 raised to the power of the shift amount. Example:

const a = 5;    // 0101 in binary
const shiftAmount = 2;
const result = a << shiftAmount;    // 10100 in binary, which is 20 in decimal

// Converting the result binary to decimal to showcase how it is 20.
// 1*2^4 + 0*2^3 + 1*2^2 + 0*2^1 + 0*2^0
// 16 + 0 + 4 + 0 + 0
// 20

In this example, the bits of a are shifted two positions to the left, resulting in the binary number 10100, which is 20 in decimal.

1. Right Shift Operator: The right shift operator (>>) shifts the bits of a number to the right by a specified number of positions. It effectively divides the number by 2 raised to the power of the shift amount. Example:

javascriptCopy codeconst a = 20;   // 10100 in binary
const shiftAmount = 2;
const result = a >> shiftAmount;    // 00101 in binary, which is 5 in decimal

In this example, the bits of a are shifted two positions to the right, resulting in the binary number 00101, which is 5 in decimal.

1. Checking Odd or Even: You can use the bitwise AND operator (&) with 1 to check whether a number is odd or even. When a number is bitwise ANDed with 1, the result will be 1 if the number is odd and 0 if the number is even. Example:

javascriptCopy codeconst number = 7;
const isOdd = number & 1;   // 00000111 & 00000001 = 00000001, which is 1 in decimal
console.log(isOdd);   // Output: 1 (true)

In this example, the number 7 is bitwise ANDed with 1, resulting in 1, indicating that the number is odd.

1. To extract the ith bit from a binary number, you can use a technique called bit masking. Here's how it works:

   • Create a mask by shifting the number 1 by i positions to the left. This sets the ith bit of the mask to 1, and all other bits to 0. Example: If you want to extract the 3rd bit (counting from 0) from a binary number, you would create the mask by shifting 1 three positions to the left: let mask = 1 << 3; // binary: 00001000

   • Apply the bitwise AND operator (&) between the original number and the mask. This operation keeps only the bits that are set to 1 in both the number and the mask, effectively extracting the ith bit.

const number = 12;   // 1100 in binary
const i = 2;
const mask = 1 << i;    // Shift 1 by 2 positions to the left: 0001 << 2 = 0100
const result = (number & mask) >> i;   // 1100 & 0100 = 0100 >> 2 = 0001, which is 1 in decimal
console.log(result);   // Output: 1

In this example, the 2nd bit of the binary number 1100 (12 in decimal) is extracted using the left shift operator and bitwise AND.

1. Real-world Applications: Bit manipulation has various real-world applications, such as optimizing code, solving specific algorithmic problems, and handling binary data efficiently. Some common applications include:

• Implementing efficient data compression algorithms.

• Performing low-level hardware operations.

• Checking and setting individual flags in bit-based configurations.

• Implementing efficient algorithms for mathematical operations, such as finding the maximum or minimum value.

Conclusion: Bit manipulation and bitwise operations provide powerful tools for working with binary data, optimizing code, and solving specific algorithmic problems efficiently. Understanding bitwise operators, left and right shift operators, techniques for checking odd or even numbers and extracting bits, handling negative numbers, and checking powers of two enables you to write more efficient and optimized JavaScript code. By leveraging these concepts, you can unlock new possibilities in your programming journey.